ゼロから作るRAW現像その４ - デモザイク処理応用編

このブログ記事「ゼロから作るRAW現像」を大きく再構成してより読みやすくした書籍「PythonとColabでできる-ゼロから作るRAW現像」を【技術書典6】にて頒布しました。

現在はBOOTHにて入手可能です。書籍+PDF版は2200円プラス送料、PDF版は1200円です。

moiz.booth.pm

はじめに
モジュールの高速化
前回のデモザイク処理の分析
より高度なデモザイク処理
より高度なデモザイク処理、実行
画像の確認
まとめ
最後に
次の記事

はじめに

これは「ゼロから作るRAW現像」という一連の記事の一つです。これらの記事の内容を前提としていますので、まだお読みでない方はこちらの記事からお読みいただくことをおすすめします。

モジュールの高速化

本題に入る前に、raw_process.pyの高速化についてです。これまでは処理の内容がわかりやすいように、画素単位で処理を書き下してきましたが、この方法ではnumpyの内部の高速性を十分に活かすことができません。

前前回までは縮小デモザイクを使っていたために画像サイズが小さく、処理速度は問題化していなかったのですが、前回縮小しないデモザイクに置き換えたために全体の処理が重くなってしまいました。

そこで、raw_process2.pyの処理をなるべくループ処理を使わず書き換えることでnumpyの恩恵を十分に使って高速化できるように書き換えて、raw_process3.pyとしました。今回以降はこのモジュールを使用します。

書き換えの内容については、画像処理的にはまったく同じで、ループの順番を替えただけなので、ここでは解説は割愛します。興味のある方はこちらをご覧ください。

raw_process/raw_process3.py at master · moizumi99/raw_process · GitHub

前回のデモザイク処理の分析

この節は、画像処理の理論的背景に興味がない方は読み飛ばして構いません。

それではまず、前回のデモザイク処理の問題点を分析してみましょう。

前回の記事の最後で、線形補間処理をFIRフィルターとして書き換える作業を行いました。これは処理の高速化を念頭においたものですが、FIRを使った画像処理として解釈することもできます。

まず、ベイヤー配列のある特定の色の画素は、もともとのフル解像度の画像に、位置によって0または１を取るサンプリング関数を画像にかけたものと解釈する事ができます。

f:id:uzusayuu:20181007145847p:plain

これを数式で表すとこうなります。

$f_{Green}(x, y) = f_{full}(x, y) \cdotp s(x, y)$

${ \displaystyle s(x, y) = \begin{cases} 0 \text{ if } x \mod 2 = y \mod 2 \\ 1 \text{ otherwise} \end{cases} }$

$s(x, y)$ はさらに

\begin{equation} s_{Green} \left ( x, y \right ) = \frac{1}{2} \left ( 1 - \left ( -1 \right ) ^ {x + y} \right ) = \frac{1}{2} \left ( 1 - e ^ {i \pi \left ( x + y \right ) } \right ) \end{equation}

となり、したがって、元の式は

\begin{equation} f_{Green} \left ( x, y \right ) = \frac{1}{2} f_{full}\left ( 1 - \left ( -1 \right ) ^ {x + y} \right ) = \frac{1}{2} \left ( f_{full} - f_{full} e ^ {i \pi \left ( x + y \right ) } \right ) \end{equation}

と表されます。この式の後半は、元の関数をx軸方向とy軸方向に $\pi$ ずつずらし、元の信号から引く事を意味します。

つまり、もし元の画像の周波数特性が模式的にこのように表されるとしたら、

f:id:uzusayuu:20181007163828p:plain

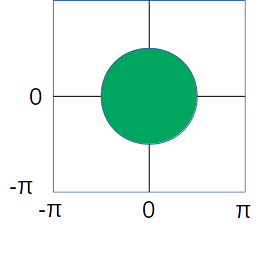
Bayer上の緑画素の周波数特性はこのようになります。

f:id:uzusayuu:20181007163915p:plain

青い部分が、全式の後半部分にできたもので、これはサンプリングによるエイリアシングを表しています。

画像の周波数成分は低い部分に多いと考えると、サンプリング前の信号を取り出すには、低周波部分を取り出してやれば良いことになります。信号処理的にはローパスフィルターをかけます。

ここで、線形補間の式から作ったFIRをフィルターを思い出すと、このような形をしていました。

[[   0, 1/4,   0],
 [ 1/4,   1, 1/4],
 [   0, 1/4,   0]]

これはそのものズバリ、ローパスフィルターです。周波数特性はこんな感じになります。

f:id:uzusayuu:20181007164819p:plain

同様に、赤画素のサンプリング関数は、

\begin{equation} s_{Red} \left ( x, y \right ) = \frac{1}{4} \left ( 1 + \left ( -1 \right ) ^ x \right ) \left ( 1 + \left ( -1 \right ) ^ y \right ) = \frac{1}{4} \left ( 1 + e ^ {i \pi x} \right ) \left ( 1 + e ^ {i \pi y} \right )
\end{equation}

で、青画素は、

\begin{equation} s_{Blue} \left ( x, y \right ) = \frac{1}{4} \left ( 1 - \left ( -1 \right ) ^ x \right ) \left ( 1 - \left ( -1 \right ) ^ y \right ) = \frac{1}{4} \left ( 1 - e ^ {i \pi x} \right ) \left ( 1 - e ^ {i \pi y} \right )
\end{equation}

エイリアシングの様子はこうなります。

f:id:uzusayuu:20181007164303p:plain

緑の画素にくらべて、エイリアシングの影響を受ける領域が大きくなっています。したがって、緑よりも強めのローパスフィルターをかける必要があることが予想されます。

前回使用した赤・青画素線形補間用ののFIRフィルターはこうなっています。

[[1/4, 1/2, 1/4],
 [1/2,   1, 1/4].
 [1/4, 1/2, 1/4]]

周波数特性はこうです。

f:id:uzusayuu:20181007164836p:plain

ちょうとエイリアシングを取り除くような特性になっています。

こうしてみると理想的なフィルター処理をしているように見えますが、実際の画像はだいぶぼやけていて、偽色という本来ないはずの色がでてきています。画像のぼやけは、もともとの画像の周波数特性を十分にカバーしていないことを、偽色の存在は本来の信号とエイリアシングとが十分に分割できていない事を示しています。このような単純な形のフィルターの限界でしょう。

より高度なデモザイク処理

この節も画像処理の理論的バックグラウンドに興味なければ読み飛ばして構いません。

この節の内容の大部分は"Frequency-Domain Methods for Demosaicking of Bayer-Sampled Color Images, Eric Dubois, IEEE Signal Processing Letters, Dec. 2005"に基づいています。

線形補間デモザイクでは各色チャンネルをそれぞれ独立なものとして処理しました。ここでは、３色のBayer配列全体を一つの画像と見てみます。

\begin{aligned} f_{bayer} = & \frac{1}{2} f_G \left ( 1 - \left ( -1 \right ) ^ {x + y} \right ) + \\ & \frac{1}{2} f_R \left ( 1 + \left ( -1 \right ) ^ {x} \right ) \left ( 1 + \left ( -1 \right ) ^ {y} \right ) + \\ & \frac{1}{2} f_B \left ( 1 - \left ( -1 \right ) ^ {x} \right ) \left ( 1 - \left ( -1 \right ) ^ {y} \right ) \end{aligned}

ここで、 \begin{equation} \left ( -1 \right ) ^ {x} = e ^ {i \pi x} \end{equation}

などを利用して、

\begin{aligned} f_{bayer} = & \left ( \frac{1}{4} f_R + \frac{1}{2} f_G + \frac{1}{4} f_B \right ) + \\ & \left ( \frac{1}{4} f_R - \frac{1}{2} f_G + \frac{1}{4} f_B \right ) \cdot e^{i \pi (x + y)} + \\ & \left ( \frac{1}{4} f_R - \frac{1}{4} f_B \right ) \cdot (e^{i \pi x} + e^{i \pi y}) \end{aligned}

まとめると

\begin{equation} \end{equation}

\begin{aligned} f_{bayer} & = f_{L} - f_{C1} e^{i \pi \left ( x + y \right ) } + f_{C2} \left ( e^{i \pi x} + e^{i \pi y} \right ) \\ f_L & = \frac{1}{4} f_R + \frac{1}{2} f_G + \frac{1}{4} f_B \\ f_{C1} & = \left ( \frac{1}{4} f_R - \frac{1}{2} f_G + \frac{1}{4} f_B \right ) \\ f_{C2} & = \left ( \frac{1}{4} f_R - \frac{1}{4} f_B \right ) \end{aligned}

逆に、 $f_L$ 、 $f_{C1}$ 、 $f_{C2}$ から、 $f_R$ 、 $f_G$ 、 $f_B$ は、

\begin{cases} f_R = f_L + f_{C1} + 2f_{C2} \\ f_G = f_L - f_{C1} \\ f_B = f_L + f_{C1} - 2f_{C2} \end{cases}

と、求められます。

では、 $f_L$ 、 $f_{C1}$ 、 $f_{C2}$ はどうやって計算すれば良いのか、というのが次の問題になります。

$f_L$ 、 $f_{C1}$ 、 $f_{C2}$ の定義をみると、 $f_R$ 、 $f_G$ 、 $f_B$ の線形結合なので、元の画像が周波数制限されていて低い周波数の成分しかもっていないとすると、 $f_L$ 、 $f_{C1}$ 、 $f_{C2}$ も周波数制限されていると考えられます。

ここで、 $f_{C1} e^{i \pi (x + y)}$ や $f_{C2} \left ( e^{i \pi x} + e^{i \pi y} \right )$ は、 $f_{C1}$ 、 $f_{C2}$ を周波数空間で $\pi$ だけシフトしたものです。もとの $f_{Bayer}$ はこれらを足し合わせたものなので、図に表すとこうなります。

f:id:uzusayuu:20181008004120p:plain

ということは、 $f_{Bayer}$ に帯域制限フィルターをかけて各成分をとりだし、周波数をシフトすれば $f_L$ 、 $f_{C1}$ 、 $f_{C2}$ を得ることがきるという事になります。

必要なフィルターは4つです。

FC1 : 縦・横ハイパスフィルター, $f_{C1}$ を取り出すのに使います。

例： \begin{equation} F_{C1} = \left(\begin{array}{c} -1 \\ 2 \\ -3 \\ 4 \\ -3 \\ 2 \\ -1\end{array}\right) \left(\begin{array}{c} -1, 2, -3, 4, -3, 2, -1\end{array}\right) \end{equation}

FC2V : 縦方向ハイパスフィルター、横方向ローパスフィルター、 $f_{C2}$ の上下の成分を取り出すのに使います。

例： \begin{equation} F_{C2V} = \left(\begin{array}{c} -1 \\ 2 \\ -3 \\ 4 \\ -3 \\ 2 \\ -1\end{array}\right) \left(\begin{array}{c} 1, 2, 3, 4, 3, 2, 1\end{array}\right) \end{equation}

FC2H: 縦方向ローパスフィルター、横方向ハイパスフィルター、 $f_{C2}$ の左右の成分を取り出すのに使います。

例： \begin{equation} F_{C2H} = \left(\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ 3 \\ 2 \\ 1\end{array}\right) \left(\begin{array}{c} -1, 2, -3, 4, -3, 2, -1\end{array}\right) \end{equation}

FL: (FC1 + FC2V + FC2H)を反転させたフィルター、 $f_{L}$ の成分を取り出すのに使います。

例 \begin{equation} F_L = 1 - F_{C1} - F_{C2V} - F_{C2H} \end{equation}

これらを使えば、

\begin{aligned} f_{C1} & = F_{C1} \left ( f_{Bayer} \right ) e^{- i \pi \left ( x + y \right )} \\ f_{C2V} & = F_{C2V} \left ( f_{Bayer} \right ) e^{-i \pi y} \\ f_{C2H} & = F_{C2H} \left ( f_{Bayer} \right ) e^{-i \pi x} \\ f_{C2} & = \left ( f_{C2V} + f_{C2H} \right ) / 2 \\ f_L & = F_L \left ( f_{Bayer} \right ) \end{aligned}

となって、 $f_L$ 、 $f_{C1}$ 、 $f_{C2}$ の近似が計算でき、そこから、 $f_R$ 、 $f_G$ 、 $f_B$ が求められるはずです。やってみましょう。

より高度なデモザイク処理、実行

まずは、必要なライブラリー郡を呼び出します。

%matplotlib inline
import numpy as np
import os
import sys
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
    sys.path.append(module_path)
import imageio
from pylab import imshow, show
import scipy
import numpy as np
import raw_process3 as raw_process

次に画像を読み込み、ホワイトバランスまでの処理を行います。

raw = raw_process.read("sample2.ARW")
color_matrix = [1141, -205, 88, -52, 1229, -154, 70, -225, 1179]
raw_array = raw_process.get_raw_array(raw)
blc_raw = raw_process.black_level_correction(raw, raw_array)
wb_raw = raw_process.white_balance_Bayer(raw, blc_raw)
dms_input = wb_raw

なお、ホワイトバランスをデモザイク先に行ったのは、前回までの各色をバラバラに処理を行うデモザイクアルゴリズムと違い、今回は３色を同時に取り扱う処理が入るため、事前に色バランスを合わせる必要があるからです。

次に必要なFIRフィルターを準備しましょう。まず、横方向のローパスフィルターです。

hlpf = np.array([[1, 2, 3, 4, 3, 2, 1]]) / 16

これを利用して、縦方向のローパスフィルターを作ります。

vlpf = np.transpose(hlpf)

同様に、横・縦方向のハイパスフィルターを作ります。

hhpf = np.array([[-1, 2, -3, 4, -3, 2, -1]]) / 16
vhpf = np.transpose(hhpf)

次に、等価フィルターを作ります。

identity_filter = np.zeros((7, 7))
identity_filter[3, 3] = 1

これらの基本的なフィルターから、必要なフィルターを作っていきます。

FC1は、縦横ハイパスフィルターなので、こうなります。

FC1 = np.matmul(vhpf, hhpf)

FC2Vは縦ハイパス・横ローパス、FC2Hは縦ローパス・横ハイパスです。

FC2V = np.matmul(vhpf, hlpf)
FC2H = np.matmul(vlpf, hhpf)

FLは、等価フィルターからFC1, FC2V, FC2Hを取り除いたものです。

FL = identity_filter - FC1 - FC2V - FC2H

これで準備ができました。

ではまず、ハイパスフィルターを使って、C1成分を周波数空間の角からとりだしてみましょう。 SciPyの２次元コンボリューション機能を使います。

# f_C1 at 4 corners
c1_mod = scipy.signal.convolve2d(dms_input, FC1, boundary='symm', mode='same')

同様に、C2V成分、C2H成分を取り出してみましょう。

c2v_mod = scipy.signal.convolve2d(dms_input, FC2V, boundary='symm', mode='same')
c2h_mod = scipy.signal.convolve2d(dms_input, FC2H, boundary='symm', mode='same')

最後にL成分をとりだします。

f_L = scipy.signal.convolve2d(dms_input, FL, boundary='symm', mode='same')

今の所、C1成分、C2V・C2H成分は、周波数空間で $\pi$ だけずれています。色情報を復元するにはこれを復調してやる必要があります。

復調するためには、 $e^{-i \pi x}$ や $e^{-i \pi y}$ を掛け合わせなくてはならないのですが、 $x$ , $y$ はいずれも整数なので、結局、 $-1$ と $1$ の繰り返しになります。つまり、 $e^{-i \pi x}$ をかけるのは奇数列の成分に-1をかける、 $e^{-i \pi y}$ をかけるのは奇数行の成分に-1をかけるのと同じです。

まずC1についてやってみましょう。必要な計算は、

\begin{equation} f_{c1} = f_{c1mod} \left ( x , y \right ) \left ( -1 \right ) ^ x \left ( -1 \right ) ^ y \end{equation}

ですので、

f_c1 = c1_mod.copy()
f_c1[:, 1::2] *= -1
f_c1[1::2, :] *= -1

となります。

同様にC2V・C2Hでは必要な計算は、

\begin{equation} f_{cv} = f_{c2vmod} \left ( x , y \right ) \left ( -1 \right ) ^ y \\ f_{ch} = f_{c2hmod} \left ( x , y \right ) \left ( -1 \right ) ^ x \end{equation}

で、プログラムは以下のようになります。

c2v = c2v_mod.copy()
c2v[1::2, :] *= -1
c2h = c2h_mod.copy()
c2h[:, 1::2] *= -1
f_c2 = (c2v + c2h) / 2

これで $f_L$ 、 $f_{C1}$ 、 $f_{C2}$ が求められました。

最後に、以下の式にしたがって $f_R$ 、 $f_G$ 、 $f_B$ を計算します。

\begin{cases} f_R = f_L + f_{C1} + 2f_{C2} \\ f_G = f_L - f_{C1} \\ f_B = f_L + f_{C1} - 2f_{C2} \end{cases}

やってみましょう。

height, width = dms_input.shape
dms_img = np.zeros((height, width, 3))
dms_img[:,:,0] = f_L + f_c1 + 2 * f_c2
dms_img[:,:,1] = f_L - f_c1
dms_img[:,:,2] = f_L + f_c1 - 2 * f_c2

これでRGB画像が再現されたはずです！残りの処理を行い結果を確認してみましょう。

img_ccm = raw_process.color_correction_matrix(dms_img, color_matrix)
rgb_image = raw_process.gamma_correction(img_ccm)

表示してみます。

outimg = rgb_image.copy()
outimg[outimg < 0] = 0
outimg = outimg / outimg.max()
imshow(outimg)

f:id:uzusayuu:20181008022550p:plain

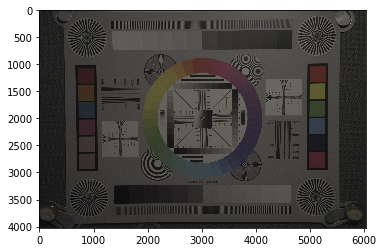
きれいに出ているようにみえます。細部は後ほど確認するとして、まずは画像をセーブしておきましょう。

raw_process.write(rgb_image, "advanced_demosaic.png")

画像の確認

では前回の線形補間による画像と画質を比べてみましょう。

f:id:uzusayuu:20181008024743p:plain:w800

左が前回の線形補完法によるデモザイク、右が今回のデモザイクです。全体にシャープさがあがっています。

別の部分の画像です。前回気になった偽色がだいぶ減っています。

f:id:uzusayuu:20181008025157p:plain:w800

シャープさの向上、偽色の低減から、今回の処理は成功のようです。

まとめ

今回は、若干複雑なデモザイク処理を画像処理のレベルから解説し、Pythonに実装しました。ここで実行した処理は、AdvancedDemosaickingDemo.ipynb としてgithubにアップロードしてあります。

また、今回の処理を新たにdemosaic()という名前のメソッドとしてraw_process3.pyに追加し、デフォルトのデモザイクアルゴリズムを置き換えました。以下の方法で今回のデモザイクアルゴリズムを使ったRAW現像が可能です。

> python3 raw_process3.py sample2.ARW test_out.png "1141, -205, 88, -52, 1229, -154, 70, -225, 1179"

参照した論文¹ではさらに、一部のチャンネルを混ぜ合わせるときに各画素毎に重み計算を行うという適合処理的アルゴリズムを扱っています。今回は割愛しましたが、興味のある方は試されてはいかがでしょうか²？

最後に

今回は応用編と銘打ってはいますが、デモザイクアルゴリズムとしてはこれでもかなりシンプルな処理の部類です。また、このアルゴリズムが発表されたのがすでに１３年前であり、これまでにさらにさまざまなアルゴリズムが提案されており、現在も進歩をつづけています³。たとえば、最近の流行はデモザイク処理にディープラーニングを使う手法です⁴。

こういった事情を考慮にいれても、今回紹介した手法はシンプルな割には高画質の出力が得られる良いアルゴリズムだと思います。私の個人的なお気に入りのアルゴリズムの一つです。

今回の内容はgithubにて公開してあります。

github.com

uzusayuu.hatenadiary.jp

Frequency-Domain Methods for Demosaicking of Bayer-Sampled Color Images, Eric Dubois, IEEE Signal Processing Letters, Dec. 2005↩
論文の著者グループがWebにてMatlabのサンプルプログラムを配布しています。また、今回のスクリプトを少し書き換えれば実現できることは確認済みです。↩
たとえば高機能なRAW現像ソフトウェアRawTherapeeではさまざまなアルゴリズムを実装しているようです。https://rawpedia.rawtherapee.com/Demosaicing/jp ↩
[1802.03769] Learning Deep Convolutional Networks for Demosaicing ↩