このブログ記事「ゼロから作るRAW現像」を大きく再構成してより読みやすくした書籍「PythonとColabでできる-ゼロから作るRAW現像」を【技術書典6】にて頒布しました。
現在はBOOTHにて入手可能です。書籍+PDF版は2200円プラス送料、PDF版は1200円です。
はじめに
これは「ゼロから作るRAW現像 」という一連の記事の一つです。 これらの記事の内容を前提としていますので、まだお読みでない方はこちらの記事からお読みいただくことをおすすめします。
「ゼロから作るRAW現像 その3 - デモザイク処理基本編」
「ゼロから作るRAW現像 その4 - デモザイク処理応用編」
「ゼロから作るRAW現像 その5 - ラズベリーパイのRAW画像処理」
「ゼロから作るRAW現像 その6 - レンズシェーディング補正」
デジタル画像のノイズ
デジタル画像にも当然ながらノイズはあります。
ノイズ源には様々な物がありますが、ごくごく大雑把に言うと、センサーから画像データを読み出す際に付加されるリードノイズと、センサーの各セルに入ってくる光の量の統計的ゆらぎによる光ショットノイズが大きな要因になります。
もちろんこれは非常に大雑把な分類で、リードノイズには、熱ショットノイズ、固定パターンノイズ、暗電流、などがあります。
光ショットノイズは光の量に依存して、その分散は次のようなポアッソン分布を取る事が知られています。
本来、光ショットノイズは光の量のみに依存するノイズのはずですが、実在する画像センサーの特性が理想的なものとは異なるために(非線形性やクロストークなど)、実際の観測では複雑な特性を見せたりします。
結局、ノイズ量も実際のセンサーやカメラ系で測定してカリブレーションする事になります。
最近のカメラ画像処理では、こういったカリブレーションによるノイズ量の推定はノイズモデルと呼ばれ重要視されています。
実際の画像のノイズ
今回の内容はgithubからJupyter Notebookのノートとしてダウンロードできます
それでは前回使用した画像のノイズを観察してみましょう。

この画像を拡大すると、このようになっています。

なんだかざらざらしています。なるべく明るくして撮影したのですが、まだだいぶノイズがのっているようです。
では実際どの程度の量のノイズがあるのか測定してみましょう。
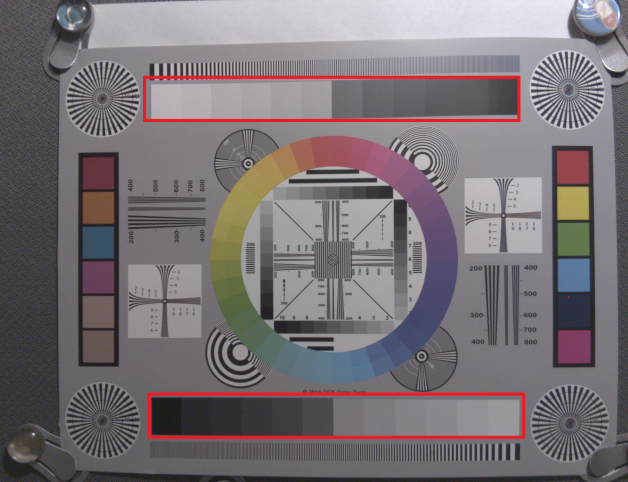
図のグレイパッチ部分(赤い長方形で囲った部分)のノイズ量を実際に測定してみます。
まず画像を前回同様の方法で読み込みます。
import os, sys, imageio, math, scipy module_path = os.path.abspath(os.path.join('..')) if module_path not in sys.path: sys.path.append(module_path) import raw_process4 as raw_process from pylab import imshow, show from matplotlib import pyplot as plt from matplotlib.pyplot import imshow import numpy as np with open("chart.jpg", "rb") as input_file: data = input_file.read() data = data[-10237440:] w = 3282 # for v1.3 w = 2592 h = 2480 - 32 # for v1.3 h = 1944 img = np.zeros((h, w)) stride = math.ceil(w * 10 / 8 / 32) * 32 for y in range(h): for x in range(w // 4): word = data[y * stride + x * 5: y * stride + x * 5 + 5] img[y, 4 * x ] = (word[0] << 2) | ((word[4] >> 6) & 3) img[y, 4 * x + 1] = (word[1] << 2) | ((word[4] >> 4) & 3) img[y, 4 * x + 2] = (word[2] << 2) | ((word[4] >> 2) & 3) img[y, 4 * x + 3] = (word[3] << 2) | ((word[4] ) & 3)
表示します。
outimg = img.copy() outimg[outimg < 0] = 0 outimg[outimg > 1023] = 1023 outimg = outimg / 1024 imshow(outimg, cmap='gray')

ブラックレベルだけ補正しておきましょう。
blacklevel = [64] * 4 bayer_pattern = np.array([[2, 1], [1, 0]]) blc_raw = raw_process.black_level_correction(img, blacklevel) outimg = blc_raw.copy() outimg = outimg.reshape((h, w)) outimg[outimg < 0] = 0 outimg = outimg / outimg.max() imshow(outimg, cmap='gray')

いつもの画像が得られました。
各グレイパッチの座標を画像ビューワーなどで測定しておきます。 今回は次のような座標でした。
patches = [(2586, 2086), (2430, 2092), (2272, 2090), (2112, 2090), (1958, 2086), (1792, 2094), (1642, 2096), (1486, 2090), (1328, 2090), (1172, 2086), (1016,2084), (860, 2084), (866, 482), (1022, 480), (1172, 476), (1328, 474), (1480, 470), (1634, 466), (1788, 462), (1944, 460), (2110, 452), (2266, 452), (2424, 448), (2586, 442)]
これらの座標((2586, 2086)など)はグレイパッチ内にとった100x100画素の正方形領域の左上の位置です。
各パッチ内の画素の分散と平均値を測定してみます。 画像のフォーマットがBayerなので、各色チャンネル毎に統計をとります。
variances = [] averages = [] for index, (dx, dy) in enumerate(((0, 0), (1, 0), (0, 1), (1, 1))): for patch in patches: x, y = patch p = blc_raw[y+dy:y+100:2, x+dx:x+100:2] s2 = (p * p).mean() av = p.mean() v = s2 - av * av variances.append(v) averages.append(av)
測定結果を見てみましょう。
plt.plot(averages, variances, linestyle='None', marker='o', color='blue') plt.show()
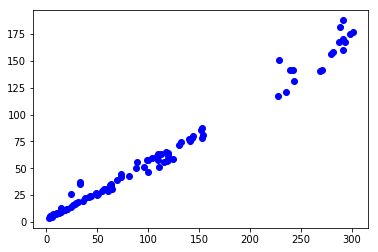
どうやら、分散は画素の値に対してほぼ線形になっているようです。
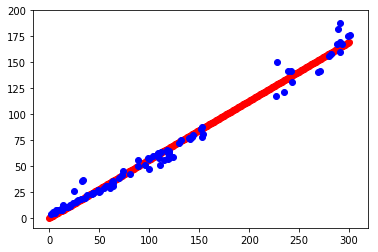
ここからこの画像では光ショットノイズが支配的だと考えられます。
ここから先はこのノイズを取り除いてくことにします。
ノイズフィルターの定番バイラテラルフィルター
ノイズフィルターに求められる特性として、ノイズは取り除いてほしいが、元の画像に含まれる情報は残しておきたい、というものがあります。
このような矛盾する要求に答えるものとしてバイラテラルフィルター1があります。
バイラテラルフィルターのアイデアは基本的に、
- ある画素の周辺の画素のうち、値が近いものは同じものだからフィルターをかける
- 値が遠いものは違うものだからフィルターをかけない。
というものです。
たとえば、各ターゲット画素のまわりに次のような5x5の領域を設定します。
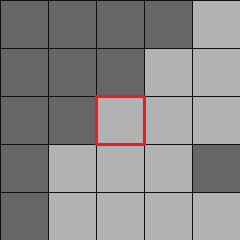
赤で囲った画素がターゲットです。
周りの画素のうち、灰色の画素はターゲットに近い値を持ち、黒い画素は大きく異なる値を持つとします。
この場合、灰色の部分は画像のある部分(たとえば新聞の地の部分)、黒い部分は他の部分(たとえば新聞の印刷部分)に含まれると考えられます。
そうなると、灰色の画素にのみフィルターをかけ、黒い画素にはフィルターをかけないことで、画像の特徴に影響を与えずにノイズフィルターをかける事ができます。
一例としてはこのようなフィルターになるでしょう。(これは説明用の図で、実際のフィルターとは異なります。)
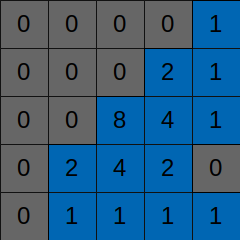
バイラテラルフィルターでは、ターゲット画素と周辺画素の一つ一つの値の差を取り、それをノイズの量とくらべて加重平均のウェイトを計算することで、ターゲット画素に近いものにのみフィルターを適用します。
式としては、例えばこうなります。
ただし、が入力画像で、
が出力画像、
が座標です。
はウィンドウのサイズ、
はチューニングパラメータで通常1以上(4から8など)です。
この式によって、ターゲット画素と周辺画素はの計算の中で比べられます。差が
に比べて大きければ
は小さくなり、その画素のウェイトは小さくなります。
逆にターゲットの差が小さい場合はの値は1に近くなり、大きなウェイトを持つことになります。
もし周辺の画像が全てターゲット画像に近い場合、フィルターの形はガウシアンフィルターに近づいていきます。
一つ注意として、ノイズ分散の扱いがあります。
通常の画像処理の教科書ではノイズ分散は画像内で一定という仮定を行います。 もしリード・ノイズが支配的ならこの仮定は正しいのですが、先程見たとおり実際の画像ではショットノイズのためにノイズの分散は画素の値に依存します。
もしノイズフィルターをかけるのがカメラ画像処理後のRGBやYUVの画像だとすると、すでにガンマ補正やローカルトーンマップ補正などの処理が行われていて、元のノイズの分布を推定するのは困難です。 RAW画像から処理する場合はこのような処理が行われていないことはわかっているので、ショットノイズなどのノイズ量を推定するのは簡単です。
次の節以降では測定したノイズの特性を利用してノイズ処理を行っていきます。
バイラテラルノイズフィルターの適用
ではこのノイズフィルターを実際の画像に適用してみましょう。
Bayerフォーマットのままではフィルターがかけにくいので、レンズシェーディング、ホワイトバランス、デモザイクを実行しフルカラー画像にします。
# Lens shading correction par = [np.array([6.07106808e-07, 9.60556906e-01]), np.array([6.32044369e-07, 9.70694361e-01]), np.array([6.28455183e-07, 9.72493898e-01]), np.array([9.58743579e-07, 9.29427169e-01])] gain_map = np.zeros((h, w)) center_y, center_x = h // 2, w // 2 for y in range(0, h, 2): for x in range(0, w, 2): r2 = (y - center_y) * (y - center_y) + (x - center_x) * (x - center_x) gain = [par[i][0] * r2 + par[i][1] for i in range(4)] gain_map[y, x] = gain[0] gain_map[y, x+1] = gain[1] gain_map[y+1, x] = gain[2] gain_map[y+1, x+1] = gain[3] lsc_raw = blc_raw * gain_map # White Balance wbg = np.array([1.128, 1, 2.546, 1]) wb_raw = raw_process.white_balance_Bayer(lsc_raw, wbg, bayer_pattern) # Demosaic dms_img = raw_process.advanced_demosaic(wb_raw, bayer_pattern)
一応確認します。
outimg = dms_img.copy() outimg = outimg.reshape((h, w, 3)) outimg[outimg < 0] = 0 outimg[outimg > 1023] = 1023 outimg = outimg / 1024 imshow(outimg)
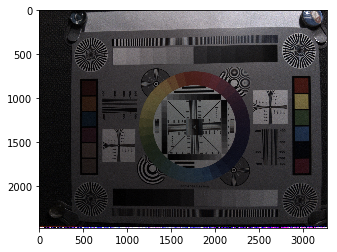
さて、このような処理を行った後でも、ノイズの分散は画素の値に比例するのでしょうか? RGBの平均に対して確かめてみましょう。
luma_img = dms_img[:, :, 0] + dms_img[:, :, 1] + dms_img[:, : , 2] variances = [] averages = [] for patch in patches: x, y = patch p = luma_img[y:y+100, x:x+100] s2 = (p * p).mean() av = p.mean() v = s2 - av * av variances.append(v) averages.append(av) plt.plot(averages, variances, linestyle='None', marker='o', color='blue') plt.show()
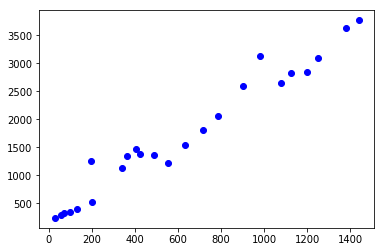
先ほどとは多少様子が違いますが、線形近似で大丈夫そうです。
傾きを求めてみましょう。
par = np.polyfit(averages, variances, 1) print(par[1]) 246.0281307576092
さあ、これでノイズフィルターを適用する準備ができました。実際にかけてみましょう。
今回はフルカラーなので、ウェイトの計算はRGBの平均に対して行い、フィルターの適用は各カラーごとに行うという方法を使っています。
コード中、coefがバイラテラルフィルターの式のに相当します。なお今回は
としました。
# 注:これは処理をわかりやすく書いたもので非常に実行速度が遅い。 # 実際にはこの後の高速版を使用することをおすすめする coef = 8 img_flt = dms_img.copy() for y in range(2, h-2): for x in range (2, w - 2): # 5x5の平均値からノイズの分散(sigma) を推定する average = luma_img[y-2:y+3, x-2:x+3].mean() sigma = par[1] * average sigma = sigma if sigma > 0 else 1 weight = np.zeros((5, 5)) out_pixel = np.zeros(3) norm = 0 # 5x5内の各画素毎に重みを計算する for dy in range(-2, 3): for dx in range(-2, 3): # 中心画素との差 diff = luma_img[y + dy, x + dx] - luma_img[y, x] diff_norm = diff * diff / sigma # 差と分散からウェイトを計算し、加重平均値を求める weight = math.exp(-coef * diff_norm) out_pixel += weight * dms_img[y + dy, x + dx, :] norm += weight # 各色毎にウェイトの和で正規化する img_flt[y, x, 0] = out_pixel[0] / norm img_flt[y, x, 1] = out_pixel[1] / norm img_flt[y, x, 2] = out_pixel[2] / norm
outimg = img_flt.copy() outimg = outimg.reshape((h, w, 3)) outimg = outimg / 1024 outimg[outimg < 0] = 0 outimg[outimg > 1] = 1 imshow(outimg)

このままではわかりにくいので、残りの処理(カラーマトリクスとガンマ補正)を行います。
ccm_matrix = (6022,-2314,394,-936,4728,310,300,-4324,8126) img_ccm = raw_process.color_correction_matrix(img_flt, ccm_matrix) img_ccm[img_ccm > 1023] = 1023 img_gamma = raw_process.gamma_correction(img_ccm, 2.2) outimg = img_gamma.copy() outimg = outimg.reshape((h, w, 3)) outimg[outimg < 0] = 0 imshow(outimg)

保存します。
raw_process.write(img_gamma, "raspi_filtered_out.png")
このファイルを画像ビューワーなどを使って拡大してノイズフィルターをかける前と比較してみるとこうなっていました。 右がノイズフィルター後です。

エッジなど画像の特徴を残したまま、平坦部分のノイズが減っている事が確認できます。
成功です。
補足:ノイズフィルター処理の高速化
最後にもう一点だけ、処理の高速化について触れます。
上記のノイズフィルターのコードはプログラムとしては動作しますが、非常に遅いコードです。
これはPythonの性能上しかたのない部分もあるのですが、numpyなどの機能を利用することでかなり改善できます。2
まず、一般的な傾向としてnumpyではループの処理は遅いので、なるべくforループを減らしたほうが高速になる場合が多いです。 numpyにはこのような用途のためにstride_tricksというライブラリ3がありますので、これを利用してループを減らしていきましょう。
まずは、RGBの平均画像(luma_img)から分散を計算します。
from numpy.lib.stride_tricks import as_strided coef = 8 average = scipy.ndimage.filters.uniform_filter(luma_img, 5, mode='mirror') sigma_map = average * par[1] sigma_map[sigma_map < 1] = 1 sy, sx = sigma_map.strides sigma_tile = as_strided(sigma_map, strides=(sy, sx, 0, 0), shape=(h, w, 5, 5)) sigma_tile = sigma_tile[2:h-2, 2:w-2, : , :]
ここではまず、3278 x 2444 通りの5x5のパッチについて、FIRフィルターを使って平均値を計算し、そこからノイズ分散をもとめています。
次にそのノイズ分散値をコピーして同じ要素の5x5の行列を作り、その5x5の行列を3278 x 2444個並べています。
同様に、各パッチの平均値をコピーして同じ要素の5x5の行列を作り、その5x5の行列を3278 x 2444個並べます。
sy, sx = luma_img.strides luma_tile = as_strided(luma_img, strides=(sy, sx, 0, 0), shape=(h, w, 5, 5)) luma_tile = luma_tile[2:h-2, 2:w-2, : , :]
次に、RGBの平均画像(luma_img)から5x5のパッチを3278 x 2444通り作ります。
sy, sx = luma_img.strides luma_box = as_strided(luma_img, strides=(sy, sx, sy, sx), shape=(h-4, w-4, 5, 5))
次に、5x5パッチ内のウェイトとその総和を3278 x 2476個分、一挙に計算します。
diff = luma_box - luma_tile weight = np.exp(-coef * diff * diff / sigma_tile) weight_sum = weight.sum(axis=(2, 3))
これで各色を処理する準備ができました。
まず、赤画素を処理します。3278 x 2444個のパッチを一度に処理します。
red = dms_img[:, :, 0] sy, sx = red.strides red_boxes = as_strided(red, strides=(sy, sx, sy, sx), shape=(h-4, w-4, 5, 5)) red_out = (weight * red_boxes).sum(axis=(2, 3)) / weight_sum
同様に、青と緑の画素を処理します。
green = dms_img[:, :, 1] sy, sx = green.strides green_boxes = as_strided(green, strides=(sy, sx, sy, sx), shape=(h-4, w-4, 5, 5)) green_out = (weight * green_boxes).sum(axis=(2, 3)) / weight_sum blue = dms_img[:, :, 2] sy, sx = blue.strides blue_boxes = as_strided(blue, strides=(sy, sx, sy, sx), shape=(h-4, w-4, 5, 5)) blue_out = (weight * blue_boxes).sum(axis=(2, 3)) / weight_sum
すべてまとめて完成です。
img_flt2 = dms_img.copy() img_flt2[2:h-2, 2:w-2, 0] = red_out img_flt2[2:h-2, 2:w-2, 1] = green_out img_flt2[2:h-2, 2:w-2, 2] = blue_out outimg = img_flt2.copy() outimg = outimg.reshape((h, w, 3)) outimg = outimg / 1024 outimg[outimg < 0] = 0 outimg[outimg > 1] = 1 imshow(outimg)
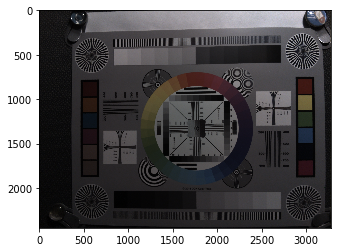
一応残りの処理も行って確認しておきます。
ccm_matrix = (6022,-2314,394,-936,4728,310,300,-4324,8126) img_ccm = raw_process.color_correction_matrix(img_flt2, ccm_matrix) img_ccm[img_ccm > 1023] = 1023 img_gamma = raw_process.gamma_correction(img_ccm, 2.2) outimg = img_gamma.copy() outimg = outimg.reshape((h, w, 3)) outimg[outimg < 0] = 0 imshow(outimg)

先ほどと同様の画像が出力されたようです。
これでノイズ処理からループが一掃されました。 処理の速度も数倍になり、実用的になりました。
まとめ
今回はノイズフィルターをとりあげ、エッジを残すノイズフィルターとしてよく使われるバイラテラル・フィルターを解説し、実装しました。
バイラテラルフィルターは移り変わりの激しい画像処理の分野では、もはや古典的ともいえるアルゴリズムです。 アルゴリズムの発表から時間が立つとはいえその基本的な考え方は現在のノイズフィルターにも受け継がれています。
とはいえ、次々に、より高性能なノイズフィルターアルゴリズムが提案されているのは間違いなく、性能もどんどん進化しています。 今回の内容で物足りない方は、BM3D4やディープラーニングを用いたノイズフィルター5など、さらに現代的なノイズフィルターアルゴリズムを実装されてはいかがでしょうか。
もう一つ重要な点として、画像内のノイズの解析と分散の推定を行い非常に簡単なノイズモデルを作成しました。 これは画像の素性のわかっているカメラ画像処理だからできることであり、このような処理ができる事がRAW現像の利点であるともいえます。 今回は光ショットノイズが支配的な画像でしたが、他のノイズが大きい画像の場合はまた違った処理が必要です。 たとえば高ISO画像(低照度画像)ではリードノイズが相対的に大きくなってきます。
また、最後にnumpyによる画像処理の高速化テクニックについても触れました。 画像処理としては本質的ではありませんが、実用上は重要な点です。
今回の内容はすべてgithubにアップロードしてあります。
入力画像: raw_process/chart.jpg at master · moizumi99/raw_process · GitHub
Jupyter Notebook上のデモ: raw_process/Raspberry_Pi_Noise.ipynb at master · moizumi99/raw_process · GitHub
ノイズフィルター後の出力画像: raw_process/raspi_filtered_out.png at master · moizumi99/raw_process · GitHub
最後に
RAW画像から始まってカメラ画像処理の内容を実践してきましたが、このノイズフィルターで終わりもだいぶ近づいてきました。
もう少しで基本的なカメラ画像処理を一通りカバーする事ができます。 もう一息です。
次の記事
-
Bilateral Filtering for Gray and Color Images, C. Tomasi and R. Manduchi, Proceedings of the 1998 IEEE International Conference on Computer Vision, pp. 839–846, 1998↩
-
ただし、処理の内容が一見わかりにくくなるというトレードオフがあります。これが理由で先程はベタ書きの処理を紹介しました。↩
-
rawpyについて教えてくれたのと同じ同僚から教わりました。感謝します。↩
-
Image and video denoising by sparse 3D transform-domain collaborative filtering | Block-matching and 3D filtering (BM3D) algorithm and its extensions↩
-
https://web.stanford.edu/class/cs331b/2016/projects/zhao.pdf↩